Funciones matemáticas. Conceptos básicos.
Muchas situaciones de la vida cotidiana y científica se expresan mediante relaciones entre dos o más entes (variables matemáticas) los cuales se escriben como una expresión matemática (fórmula), así por ejemplo Newton al escribir la segunda ley de la mecánica que lleva su nombre, escribió que “la fuerza neta que actúa sobre una partícula de masa \(m\) es igual al cambio en su momentum lineal” lo cual matemáticamente se escribe como \(F=∆p\), donde \(p\) es el momento lineal y se escribe en función del producto de la masa de la partícula por su velocidad \(p=mv\).
Otro ejemplo es el área de un rectángulo, el cual se escribe en función de las longitudes de su ancho y largo como \(A=wl\), pero ¿qué es una función matemática?
Prodcuto cartesiano
En el álgebra se estudió el concepto de conjunto y se verificó que dados dos conjuntos \(A\) y \(B\) no vacíos, el producto cartesiano \(A\times B\) de ellos es el conjunto de todos los pares ordenados \(\left(x,y\right)\) tales que \(x \in A\) y \(y \in B\), por ejemplo, si \(A=\left\{1,\ 2 \right\}\) y \(B=\left\{e,\ i,\ o,\ u\right\}\) el producto cartesiano \(A\times B=\left\{\left(1,\ e\right),\left(1,\ i\right),\ \left(1,\ o\right),\left(1,\ u\right),\left(2,e\right),\left(2,i\right),\left(2,o\right),\left(2,u\right)\right\}\).
Al indicar que existe una relación en la cual un elemento \(x\) de un conjunto de partida \(A\) se relaciona con un elemento y de un conjunto de llegada \(B\) se escribe \(\mathcal{R}:x\longrightarrow y\) lo cual se lee “\(x\) está relaciona con \(y\)”. Así si pide por ejemplo una relación \(\mathcal{R}:x\longrightarrow~~ y~~\forall\left(x,y\right)~|~y\) es una vocal cerrada, subconjunto del producto cartesiano anterior, se tiene: \(\mathcal{R}=\left\{\left(1,\ i\right),\left(1,\ u\right),\left(2,i\right),\left(2,u\right)\right\}\).
De donde se dice que “uno está relacionado con \(i\)” lo cual se escribe \(\mathcal{R}:1\longrightarrow i\) bajo la relación dada. Una función es un subconjunto del producto cartesiano de dos conjuntos no vacíos, la cual cumple con cierta condición.
Definición de función en variable real.
Dados dos conjuntos \(X\) y \(Y\) no vacíos, subconjuntos de \(\mathbb{R}\), se dice que una función en variable real, es una relación que asigna a cada elemento de un conjunto de partida, un único elemento del conjunto de llegada. Donde \(X\) es el conjunto de partida y \(Y\) es el conjunto de llegada. La notación de función es \(f\left(x\right)\) la cual se lee “efe de \(x\)”.
Para comprender la definición de función piense lo siguiente, desde muy “temprano” en el estudio de la geometría se enseña que el área de un círculo está relacionada con su radio mediante la expresión \(A=\pi r^2\) de donde para cada valor de \(r\) existe un uníco valor de \(A\). Ahora imagine que para un valor r de un radio cualquiera existiera más de un valor \(A\) para el área. ¿Es posible tener más de una respuesta para un valor de \(r\)?
Ampliando el concepto, piense en la composición de un estado democrático presidencialista, a cada Estado le corresponde un único presidente, de modo que cada ministro se relaciona con un único presidente. Imagine lo que pasaría si existiera más de un presidente ¿Con cuál de ellos debe relacionarse un ministro en tal caso?
estado democrático presidencialista, a cada Estado le corresponde un único presidente, de modo que cada ministro se relaciona con un único presidente. Imagine lo que pasaría si existiera más de un presidente ¿Con cuál de ellos debe relacionarse un ministro en tal caso?
Formas de representar una función.
\(1.\) Mediante una descripción verbal.
\(2.\) Por medio de una expresión matemática.
\(3.\) A través de una tabla de valores o conjunto de pares ordenados.
\(4.\) De manera visual por medio de gráficas.
Note que la definición de función expresa “a cada elemento de un conjunto de partida un único elemento de un conjunto de llegada”
piense en una función como en la gráfica de relación ministros-presidente, si un ministro se relaciona con más de un presidente no funciona (a quien debe obedecer el ministro, o quien autoriza los fondos), de modo que desde un ministro cualquiera debe salir una y solo una flecha que llega hasta el presidente \(p\).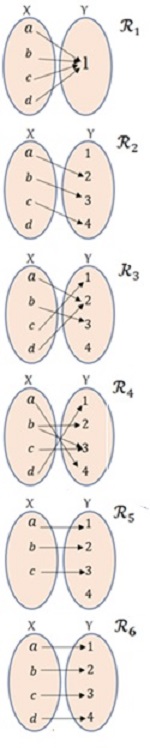 Además, ningún ministro puede quedarse sin relacionarse con el presidente (no puede hacer lo que desee, tiene un superior), por tanto, en el conjunto de los ministros debe salir una flecha de cada uno de sus elementos. La gráfica muestra varias relaciones de las cuales no todas son funciones.
Además, ningún ministro puede quedarse sin relacionarse con el presidente (no puede hacer lo que desee, tiene un superior), por tanto, en el conjunto de los ministros debe salir una flecha de cada uno de sus elementos. La gráfica muestra varias relaciones de las cuales no todas son funciones.
\(\mathcal{R}_1\) es una función, cumple con la definición todos los \(x\) se relacionan con un \(y\).
\(\mathcal{R}_2\) no es una función, no cumple con la definición, un \(x\) no se relaciona.
\(\mathcal{R}_3\) es una función, cumple con la definición, todos los \(x\) se relacionan con algún \(y\).
\(\mathcal{R}_4\) no es una función, \(b\) se relaciona con más de un \(y\).
\(\mathcal{R}_5\) es una función, cumple con la definición, todos los \(x\) se relaciona con algún \(y\).
\(\mathcal{R}_6\) es una función, cumple con la definición, todos los \(x\) se relaciona con algún \(y\).
Para más contenidos de funciones clic en y luego clic en la pestaña del contenido deseado.
Clasificación segun el tipo.
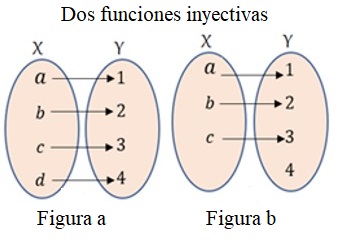
De acuerdo con el tipo de relación que hay en una función estas se pueden clasificar de distintas maneras, se dice que una función es inyectiva o uno a uno si todos los elementos del conjunto de partida se relacionan con un elemento distinto del conjunto de llegada (como en la figura).
Si todo elemento del conjunto de llegada es imagen de al menos un elemento del dominio, se dice que la función es sobreyectiva. Si una función es inyectiva y a la vez sobreyectiva se dice que es biyectiva ver figura a. La figura b no es biyectiva porque no es sobreyectiva (ningún \(x\) se relaciona con el 4).
Se dice que dos funciones son inversas cuando el dominio de una es el rango de la otra. Las funciones inversas se estudiarán más adelante.
Según su estructura las funciones pueden ser
$$\left\{\begin{array}{l}{\rm algebraicas}\left\{\begin{array}1{\rm polinomicas}\left\{\begin{array}{l}{\rm constante:}~y=k\\{\rm lineales:}y=mx+n\\{\rm cuadrácticas:}~y=ax^2+bx+c\\{\rm de~ grado}\ n>2:y=a x^n+\cdots\end{array}\right.\\{\rm racionales:}y=\frac{P\left(x\right)}{Q\left(x\right)}\ \ \ \ {\rm donde}\ Q\left(x\right)\neq0\ \\{\rm irracionales:poseen~radicales~} {\rm irreducibles}\end{array}\right.\\{\rm trascendentes}\left\{\begin{array}{l}{\rm trigonométricas}\\{\rm logaritmicas}\\{\rm exponenciales}\end{array}\right.\\{\rm a~ trozos:~funciones~definidas~por~tramos.}\end{array}\right.$$
Algunos ejemplos de funciones polinómicas.
Funciones constantes (grado cero): como \(f\left(x\right)=1\).
Funciones lineales (grado uno), \(y=mx+n\Longrightarrow y=3x+5\)
Funciones cuadráticas (grados dos):
\(y=a\left(x-h\right)^2+k\Longrightarrow y=3{(x-5)}^2+7\) que también puede ser escrita en la forma \(f(x)=ax^2+bx+c\) como \(f(x)=3x^2-30x+82\)
Funciones polinomiales de grado mayor que dos, ejemplo \(y=x^3-7x+5\) o \(y=x^4+5x+8\)
Funciones a trozos (o por tramos), por ejemplo, una factura telefónica como sigue, donde \(t\) se mide en minutos. $$f(t)=\left\{\begin{array}{l}400~~~~\mathrm{si}~0 < t\leq 100\\400+1.75t~~~~\mathrm{si}~0< t\leq 100\\575+1.25(t-100)~~~~\mathrm{si}~ 100< t\end{array}\right.$$ Para más contenidos sobre funciones clic en y luego clic en la pestaña del contenido deseado.
Evaluación de funciones
Evaluar una función es encontrar la imagen que produce un determinado valor de la variable independiente. Así, si se desea determinar el valor de \(y=f(x)\) para \(x=3\) se sustituye \(x\) por \(3\) en en \(f(x)\) y se realizan las operaciones indicadas, como en los ejemplos siguientes.
Ejemplo 1. Evaluar la función \(f\left(x\right)=2x^2+5x+1\) para \(x=\textcolor{#ff0080}{0},\) \(x=\textcolor{#ff0080}{3}\) y \(x=\textcolor{#ff0080}{5}\).
\(f\left(\textcolor{#ff0080}{0}\right)=2\left(\textcolor{#ff0080}{0}\right)^2+5\left(\textcolor{#ff0080}{0}\right)+1=1\)
\(f\left(\textcolor{#ff0080}{3}\right)=2\left(\textcolor{#ff0080}{3}\right)^2+5\left(\textcolor{#ff0080}{3}\right)+1=34\)
\(f\left(\textcolor{#ff0080}{5}\right)=2\left(\textcolor{#ff0080}{5}\right)^2+5\left(\textcolor{#ff0080}{5}\right)+1=76\)
Ejemplo 2. Evaluar la función \(y=x^2-5x+3\) para \(x=\textcolor{#ff0080}{x^2},\) \(x=\textcolor{#ff0080}{1/x}\) y \(x=\textcolor{#ff0080}{-x}.\)
Solución:
\begin{align}
y\left(\textcolor{#ff0080}{x^2}\right)&=\left(\textcolor{#ff0080}{x^2}\right)^2-5\left(\textcolor{#ff0080}{x^2}\right)+3=x^4-5x^2+3\\
y\left(\textcolor{#ff0080}{\frac{1}{x}}\right)&=\left(\textcolor{#ff0080}{\frac{1}{x}}\right)^2-5\left(\textcolor{#ff0080}{\frac{1}{x}}\right)+3=\frac{1}{x^2}-\frac{5}{x}+3\\
y\left(\textcolor{#ff0080}{-x}\right)&=\left(\textcolor{#ff0080}{-x}\right)^2-5\left(\textcolor{#ff0080}{-x}\right)+3=x^2+5x+3\\
\end{align}
Ejemplo 3. Evaluar \(f\left(x\right)=3x^2+2x+3\) para \(x=\textcolor{#ff0080}{x+h}.\)
\(f\left(\textcolor{#ff0080}{x+h}\right)=3\left(\textcolor{#ff0080}{x+h}\right)^2+2\left(\textcolor{#ff0080}{x+h}\right)+3\)
\(f\left(\textcolor{#ff0080}{x+h}\right)=3\left(\textcolor{#ff0080}{x^2+2hx+h^2}\right)+2\textcolor{#ff0080}{x}+2\textcolor{#ff0080}{h}+3\)
\(f\left(\textcolor{#ff0080}{x+h}\right)=3x^2+6hx+3h^2+2x+2h+3\)
Ejemplo 4. Evaluar \(y=\sin{x}\) para: \(x=\textcolor{#ff0080}{30°},~~ x=\textcolor{#ff0080}{60°}~~ y~~ x=\textcolor{#ff0080}{90°}.\)
Solución: sustituyendo \(x\) por cada uno de los valores dados.
\begin{align}
&y(\textcolor{#ff0080}{30°})=\sin{ \textcolor{#ff0080}{30°}}=1/2\\
&y(\textcolor{#ff0080}{60°})=\sin{ \textcolor{#ff0080}{60°}}=\sqrt{3}/2\\
&y(\textcolor{#ff0080}{90°})=\sin{ \textcolor{#ff0080}{90°}}=1\end{align}
Ejemplo 5 Funcion por tramo. Evaluar la función por tramo
$$f(t)=\left\{\begin{array}{l}
f\left(t\right)=400~~~~~\mathrm{si}~ t=0~~~~~~~~~~~\\
400+1.75t~~~\mathrm{si} ~ 0< t≤100\\
575+1.25(t-100)~~~~\mathrm{si}~ 100< t\\
\end{array}\right.$$
para los valores \(t=\textcolor{#ff0080}{90};~~\\ t=\textcolor{#ff0080}{100};~~ \\ t=\textcolor{#ff0080}{201}.\)
Solución: para \(t=90\) y \(t=100\) la función \(f\left(t\right)\) está definida por el segundo tramo, mientras que para \(t=201\) la función está definida en el tercer tramo, de donde se tiene:
$$f(t)=\left\{\begin{array}{l}
f\left(\textcolor{#ff0080}{90}\right)=400+1.75(\textcolor{#ff0080}{90})=557.5\\
f\left(\textcolor{#ff0080}{100}\right)=400+1.75(\textcolor{#ff0080}{100})=575\\
f\left(\textcolor{#ff0080}{201}\right)=575+1.25(\textcolor{#ff0080}{201})=701.25\\
\end{array}\right.$$
Operaciones básicas de funciones.
Sean \(f(x)\), \(\mathrm{g}(x)\) y \(h(x)\) tres funciones cualquiera definidas en \(\mathbb{R}\), entonces las operaciones básicas (adición, sustracción, multiplicación, división, potenciación y radicación) se definen al igual que las operaciones básicas algebraicas de polinomios, siempre que dicha operación esté definida.
Ejemplo 1. Sea \(f(x)=2x-3\) y sea \(\mathrm{g}(x)=5x-1\) determinar \(f(x)+\mathrm{g}(x).\)
Solución: \(f(x)+{\rm g}(x)=(f+{\rm g})(x)=2x-3+5x-1=7x-4.\)
Ejemplo 2. Dada \(f\left(x\right)=4x-5\) y \({\rm g}(x)=3x^2-4x+5\) determinar \(f(x)\cdot{\rm g}(x)\)\begin{align} &f(x)\cdot {\rm g}(x)=4x(3x^2-4x+5)-5(3x^2-4x+5)\\ &f(x)\cdot {\rm g}(x)=12x^3-16x^2+20x-15x^2+20x-25\\ &f(x)\cdot {\rm g}(x)=12x^3-31x^2+40x-25 \end{align}
Ejemplo 3. Dadas las funciones
$$f(x)=\frac{3x}{5x+2}~~{\rm y}~~~~{\rm g}(x)=\frac{4}{3x+1}$$ determinar \((f-{\rm g})(x)\).
Solución:
\begin{align}
&\left(f-{\rm g}\right)\left(x\right)=\frac{3x\left(3x+1\right)-4\left(5x+2\right)}{\left(5x+2\right)\left(3x+1\right)}=\frac{9x^2+3x-20x-8}{\left(5x+2\right)\left(3x+1\right)}\\
&\left(f-\mathrm{g}\right)\left(x\right)=\frac{9x^2-17x-8}{\left(5x+2\right)\left(3x+1\right)}\end{align}
Ejemplo 4. Sean las funciones
$$f\left(x\right)=\frac{3x}{2x+3};\ {\rm g}(x)=\frac{4}{3x+1}\ y\ \ h\left(x\right)=\frac{5x}{2x-1}$$ Determinar \((f-{\rm g}+h)(x)\)
Solución: sea \(S\) la suma buscada, entonces,
\begin{align}
&S=\frac{3x\left(3x+1\right)\left(2x-1\right)-4\left(2x+3\right)\left(2x-1\right)+5x\left(2x+3\right)\left(3x+1\right)}{\left(2x+3\right)\left(3x+1\right)\left(2x-1\right)}\\
&S=\frac{18x^3-3x^2-3x-16x^2-16x+12+30x^3+55x^2+15x}{\left(2x+3\right)\left(3x+1\right)\left(2x-1\right)}\\
&S=\frac{48x^3+36x^2-4x+12}{\left(2x+3\right)\left(3x+1\right)\left(2x-1\right)}\end{align}
Composición de funciones.
Sean \(f(x)\) y \(\mathrm{g}(x)\) dos funciones reales cualesquiera, entonces se define una nueva función llamada “\(f\) compuesta \(\mathrm{g}\) de \(x\)” o simplemente “\(f\) compuesta \(\mathrm{g}\)” denotada por \((f\circ \mathrm{g})(x),\) la cual resulta al evaluar la función \(f(x)\) en \(\mathrm{g}(x).\)
Definición de función compuesta.
$$\left(f\circ \mathrm{g}\right)(x)=f\left({\rm g}(x)\right)$$
Ejemplo 1. Dadas las siguientes funciones \(f(x)=\sqrt{x+3}\) y \(\mathrm{g}(x)=\textcolor{#ff0080}{3x^2+5}.\) Determinar las funciones compuestas.
$$1.\ \ \left(f\circ \mathrm{g}\right)\left(x\right)~~~ {\rm y}~~ 2.\ \left(\mathrm{g}\circ f\right)\left(x\right)$$
¿Cuál es la conclusión que se infiere del resultado?
Solución: Para \(\left(f\circ \mathrm{g}\right)\left(x\right)\) sustituir \(x\) por \(\mathrm{g}\left(x\right)\) en \(f\left(x\right)\)
$$\left(f\circ \mathrm{g}\right)\left(x\right)=\sqrt{\textcolor{#ff0080}{3x^2+5}+3}=\sqrt{3x^2+8}$$
Para \(\left(g\circ f\right)\left(x\right)\) sustituir \(x\) por \(f\left(x\right)\) en \(\mathrm{g}\left(x\right)\)
$$\left(\mathrm{g}\circ f\right)\left(x\right)
=3 \left(\textcolor{#ff0080}{\sqrt{x+3}}\right)^2+5$$
$$\left(\mathrm{g}\circ f\right)\left(x\right)
=3(x+3)+5=3x+14$$
Al comparar los resultados se puede inferir que
$$\left(f\circ \mathrm{g}\right)\left(x\right)\neq\left(\mathrm{g}\circ f\right)\left(x\right)$$
y por tanto, la composición de funciones no es conmutativa.
Otras propiedades de la composición de funciones que se pueden determinar al igual que la anterior son, la propiedad asociativa, propiedad del elemento neutro y la propiedad de la inversa.
Composición de más de dos funciones.
Al realizar la composición de más de dos funciones, como por ejemplo \(\left(f\circ \mathrm{g}\circ h\right)\left(x\right)\) basta con no cambiar de lugar ninguna de las funciones (el orden importa). Una regla básica para llegar al camino es trabajar la composición desde la derecha hacia la izquierda, como sigue:
Composición de tres funciones.
$$\left(f\circ \mathrm{g}\circ h\right)\left(x\right)=f\left(\mathrm{g}\left(h\left(x\right)\right)\right)$$ Ejemplo 2. Prueba de la propiedad asociativa. Dadas las funciones \(f\left(x\right)=\sqrt{x+3};~~\mathrm{g}=3x^2+5,\) y \(h\left(x\right)=1-2x\) determinar, $$\left(f\circ \mathrm{g}\right)\left(h\left(x\right)\right)~~y~~ f\left(\mathrm{g}\left(h\left(x\right)\right)\right)=f\left(\left(\mathrm{g} \circ h\right)\left(x\right)\right).$$ Solución: del ejemplo anterior \(\left(f\circ \mathrm{g}\right)\left(x\right)=\sqrt{3x^2+8},\) evaluando la función compuesta en \(h\left(x\right)=1-2x\) se tiene, $$\left(f\circ \mathrm{g}\circ h\right)\left(x\right)= \sqrt{3\left(1-2x\right)^2+8}= \sqrt{12x^2-12x+11}$$ Para \(f\left(\left(\mathrm{g}\circ h\right)\left(x\right)\right)\) se tiene, $$\left(\mathrm{g}\circ h\right)\left(x\right)=3\left(1-2x\right)^2+5=12x^2-12x+8,$$ al evaluar \(f(x)\) es este valor se tiene $$f\left(\left(g\circ h\right)\left(x\right)\right)=\sqrt{12x^2-12x+8+3}=\sqrt{12x^2-12x+11}$$ lo cual prueba la propiedad asociativa de la composición de funciones.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.